Плоттерное искусство и алгоритмы

В этом посте решил стремиться к чему-то более сложному, попытаться разработать алгоритм с нуля. Я называю этот алгоритм «лоскутным одеялом», хотя и не утверждаю, что изобрел его. Я уверен, что многие до меня обнаружили тот же алгоритм.

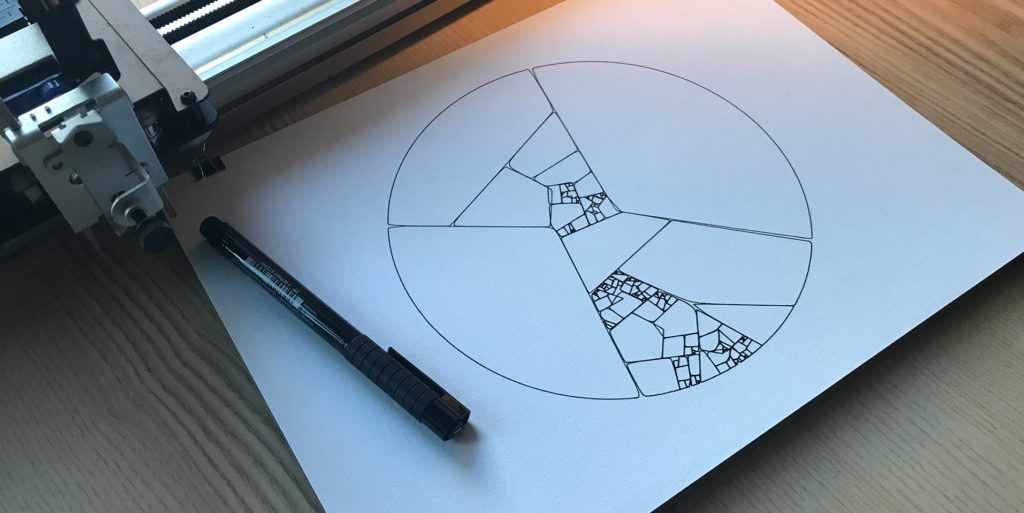
Алгоритм, который мы попытаемся реализовать, работает следующим образом:

1. Начнём с набора из N исходных точек.
2. Выберите группу точек и нарисуйте выпуклую оболочку, которая окружает их все.
3. Удалите точки, содержащиеся в выпуклой оболочке из нашего набора данных.
4. Повторите процедуру с шага 2.

«Выпуклая оболочка» — это выпуклый многоугольник, который инкапсулирует набор точек; это немного похоже на то, как если бы мы забивали гвозди в каждой точке, а затем наматывали вокруг них нитку, чтобы создать замкнутую форму.

Чтобы выбрать кластер, мы будем использовать известный алгоритм k-means для разделения данных на N кластеров, а затем выберите тот кластер, который имеет наименьшее количество точек. Вероятно, есть много способов случайного выбора кластеров, возможно, более оптимально, чем с k-means.

Первоначальная настройка

Сначала установите необходимые библиотеки, а затем создайте новый скрипт с помощью penplot. (доступен на GitHub)

# install dependencies
npm install density-clustering convex-hull

# generate a new plot
penplot patchwork.js --write --open

Теперь, давайте начнем с добавления одного и того же кода из части 1 и вызовем функцию (update) для обновления для нашего алгоритма. Нам также нужно вернуть { animate: true }, чтобы penplot запустил цикл рендеринга, а не просто рисовал один кадр.

// ...

import { PaperSize, Orientation } from 'penplot';
import { randomFloat } from 'penplot/util/random';
import newArray from 'new-array';
import clustering from 'density-clustering';
import convexHull from 'convex-hull';

export const orientation = Orientation.LANDSCAPE;
export const dimensions = PaperSize.SQUARE_POSTER;

export default function createPlot (context, dimensions) {
  const [ width, height ] = dimensions;

  // A large point count will produce more defined results
  const pointCount = 500;
  let points = newArray(pointCount).map(() => {
    const margin = 2;
    return [
      randomFloat(margin, width - margin),
      randomFloat(margin, height - margin)
    ];
  });

  // We will add to this over time
  const lines = [];

  // The N value for k-means clustering
  // Lower values will produce bigger chunks
  const clusterCount = 3;

  // Run our generative algorithm at 30 FPS
  setInterval(update, 1000 / 30);

  return {
    draw,
    print,
    background: 'white',
    animate: true // start a render loop
  };

  function update () {
    // Our generative algorithm...
  }

  // ... draw / print functions ...
}

Вы ничего не увидите, если запустите код, потому что наш массив строк пуст. Если бы мы визуализировали наши случайные точки, они выглядели бы так:

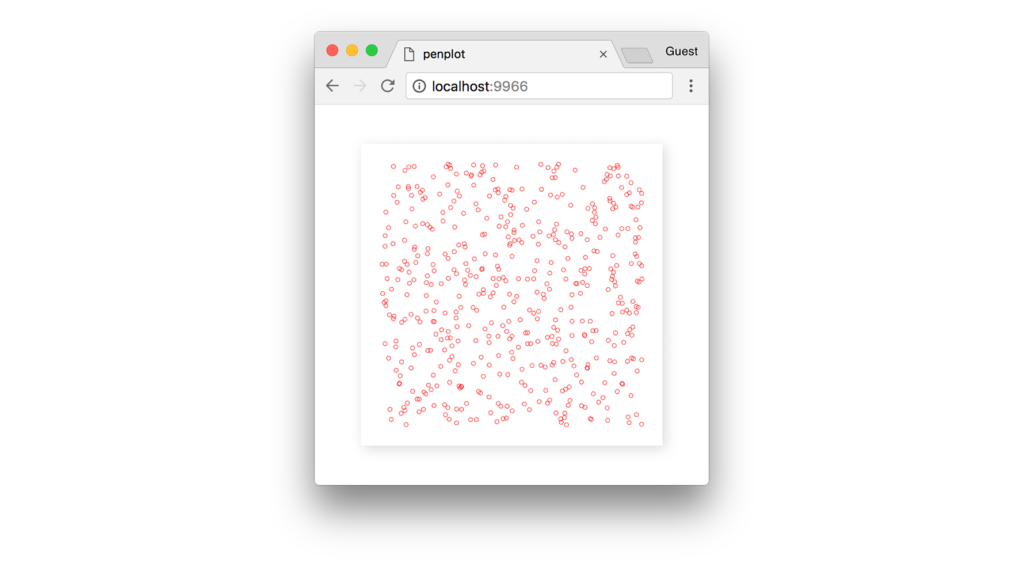
Давайте сделаем так, чтобы при каждом запуске функции (update) в массив lines добавлялся новый полигон. Вторым шагом в нашем алгоритме является выбор кластера точек из нашего набора данных. Для этого мы будем использовать модуль кластеризации плотности, фильтруя результаты, чтобы убедиться, что мы выбираем кластер с не менее чем 3 точками. Затем мы сортируем по возрастанию плотности, чтобы выбрать кластер с наименьшим количеством точек (т. е. первым).

Как с triangulate() , кластеризация плотности возвращает списки индексов, а не точек, поэтому нам нужно сопоставить индексы с их соответствующими позициями.

function update () {
  // Not enough points in our data set
  if (points.length <= clusterCount) return;

  // k-means cluster our data
  const scan = new clustering.KMEANS();
  const clusters = scan.run(points, clusterCount)
    .filter(c => c.length >= 3);

  // Ensure we resulted in some clusters
  if (clusters.length === 0) return;

  // Sort clusters by density
  clusters.sort((a, b) => a.length - b.length);

  // Select the least dense cluster
  const cluster = clusters[0];
  const positions = cluster.map(i => points[i]);

  // ...
}

Теперь, когда у нас есть кластер, мы можем найти выпуклую оболочку его точек и удалить эти точки из нашего исходного набора данных. Модуль выпуклой оболочки возвращает список (edges) (т. е. линейных сегментов), и, взяв первую вершину в каждом ребре, мы можем сформировать замкнутую полилинию (многоугольник) для этого кластера.

function update () {
  // Select a cluster
  // ...

  // Find the hull of the cluster
  const edges = convexHull(positions);

  // Ensure the hull is large enough
  if (edges.length <= 2) return;

  // Create a closed polyline from the hull
  let path = edges.map(c => positions[c[0]]);
  path.push(path[0]);

  // Add to total list of polylines
  lines.push(path);

  // Remove those points from our data set
  points = points.filter(p => !positions.includes(p));
}

Ниже мы видим множество синих точек (кластер) и их выпуклую оболочку, определяемую вокруг них.

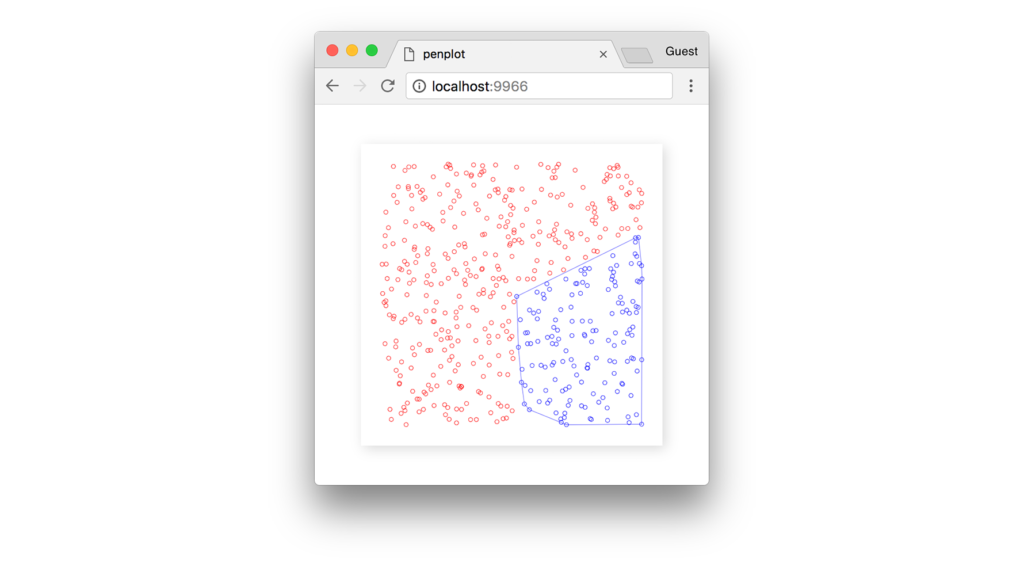
Как только точки из этого кластера удаляются из набора данных, мы остаемся с многоугольником на их месте.

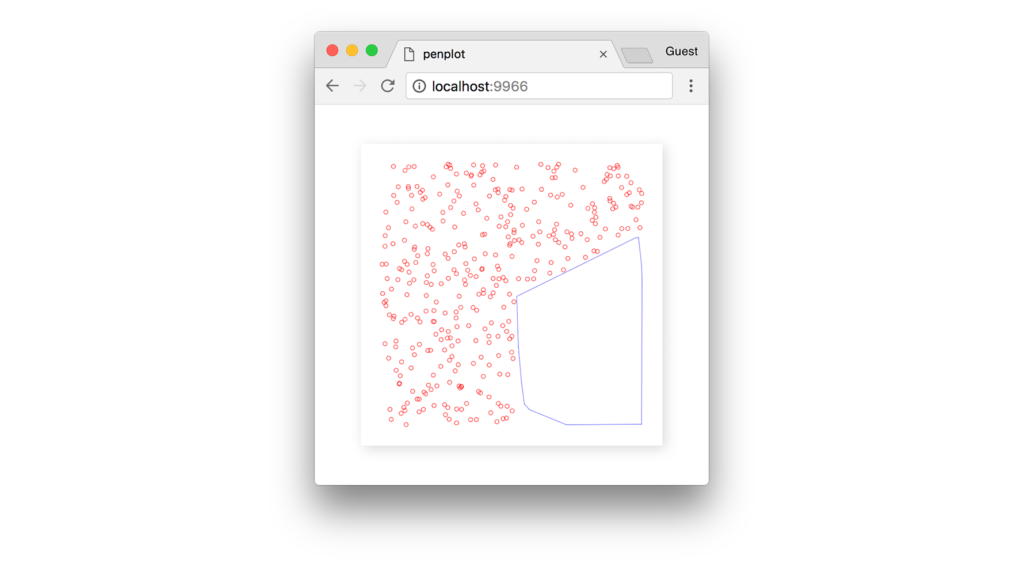
По мере продвижения алгоритма вперед мы получаем все больше полигонов, заполняющих пустое пространство.

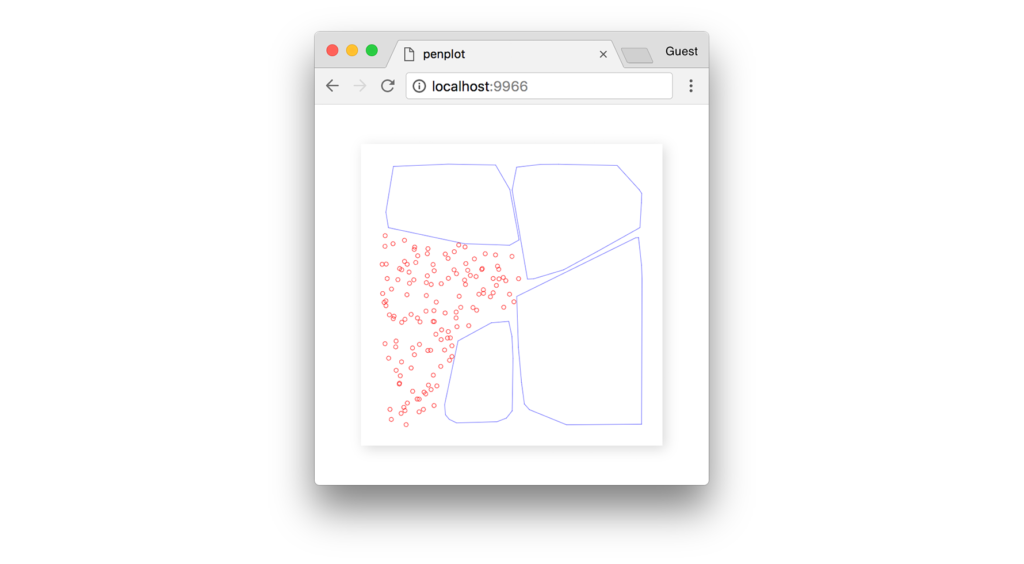
Пока в конце концов алгоритм не сойдется, и мы не сможем найти более подходящие кластеры.

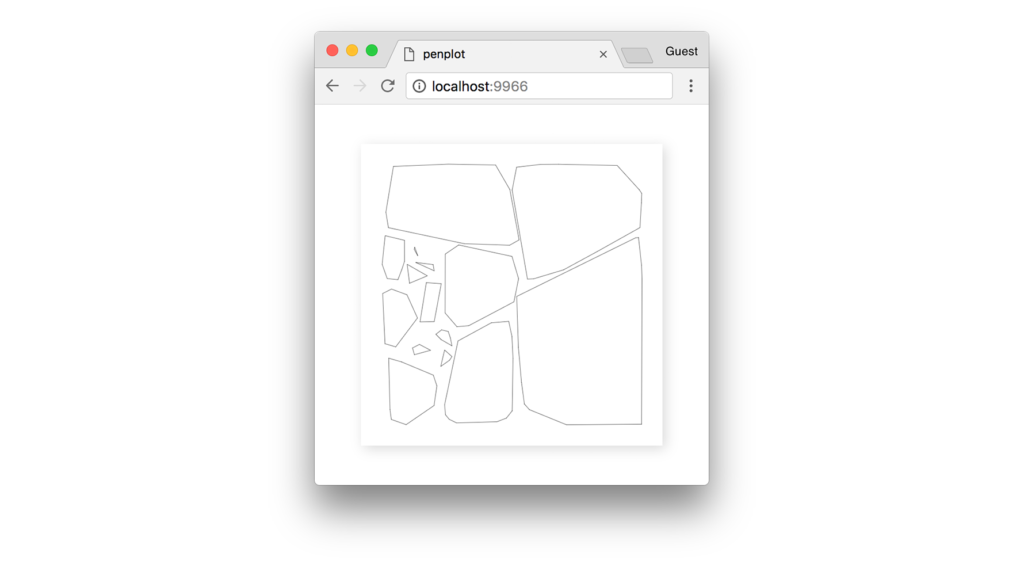
Давайте увеличим количество точек, чтобы получить более точный результат. С большим числом, например, 50 000 точек, мы получим более подробные и более гладкие полигоны.

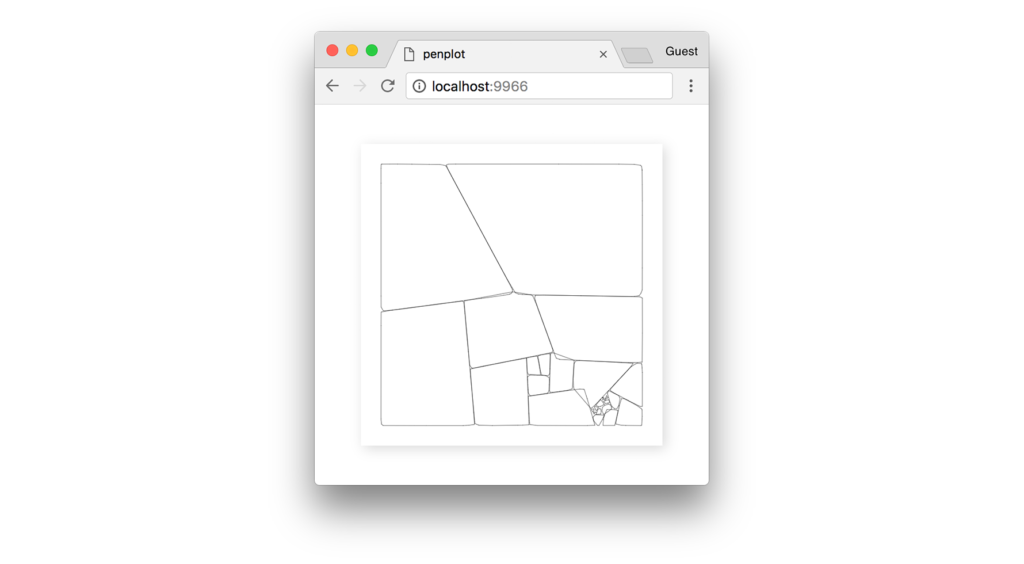
Это ещё не всё. Дальше — больше) В следующей части покажу как эту мозаику сложить внутри сложных объектов, читайте Плоттерное искусство. Часть 2.